Research Home Meet the Group Join the Group Current Projects Molecular-Genetic Origins of Multicellularity Novel Computational Approaches to Predict Misfolding-specific Epitopes and Design Precision Immunotherapeutics for Neurodegenerative Disease Protein Misfolding & Aggregation Other Projects In Silico Mechanical Manipulation of Misfolding-Prone Proteins Insights into DNA Structure and Dynamics Through Coarse-Grained Models Dielectric Properties of Proteins Role of Osmolytes and Denaturants on Protein Stability Generalization of Distance to High-Dimensional Objects Special Topics in Biophysics

Generalization of Distance to High-Dimensional Objects

We have recently worked out the equations governing the distance between two space curves, such as those shown below.

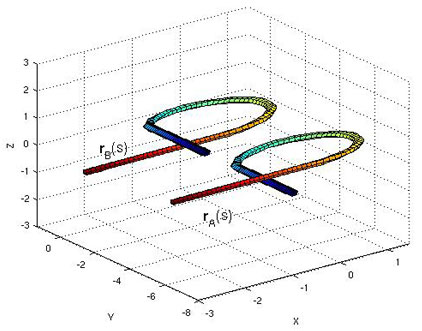
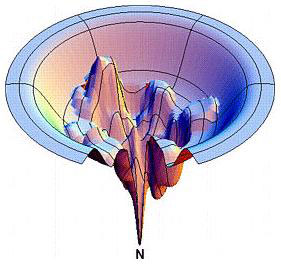
This is a nonlinear PDE with Lagrange functional constraints. The usefulness of such a metric is to answer such questions as "what is the distance from a random walk configuration to this (smoothed) protein structure:

Another example, "what do the X and Y axes mean in this diagram of the protein folding funnel?"

Do you know how to move a piece of string from configuration r_A(s) to configuration r_B(s) while traveling the minimal amount of distance?

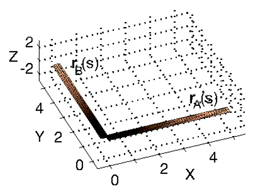
See
Plotkin, S. S. “Generalization of distance to higher dimensional objects”, Proc Nat Acad Sci USA. 104 14899-14904 (2007).
for the answer!

This shows the minimal transformation to an alpha helix.

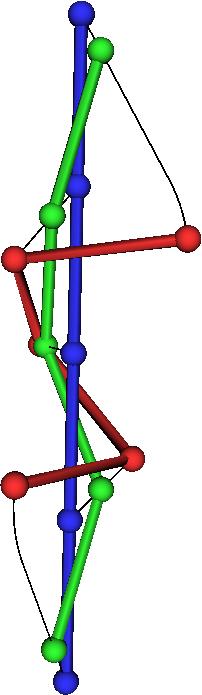...and to a beta hairpin:

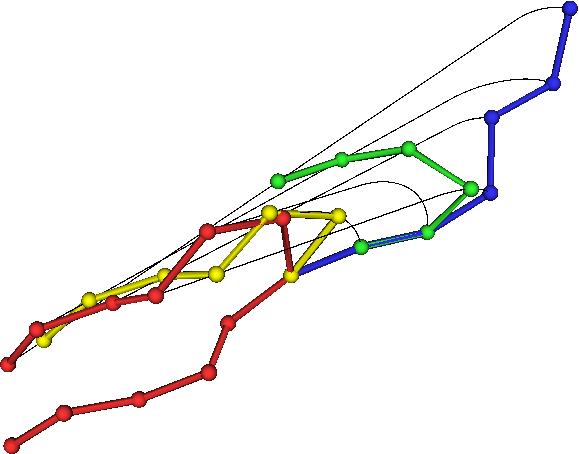
In it's simplest form, the equation for the transformation using up the minimal amount of motion looks like this:

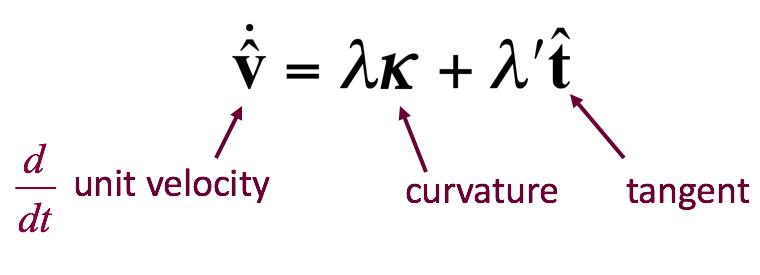
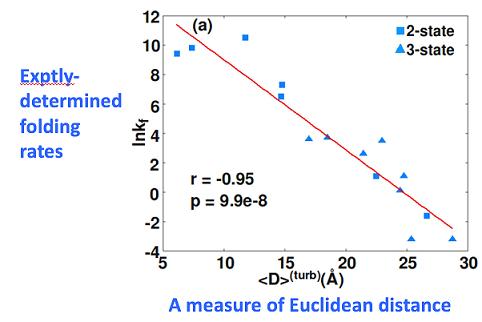
and an approximation to it, correlates remarkably well with how long it takes a protein to fold up:

When knotting or chain non-crossing becomes important, things get tricky:

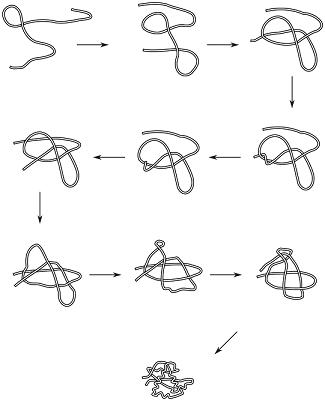
We can actually look at the taxonomy of folding transformations:

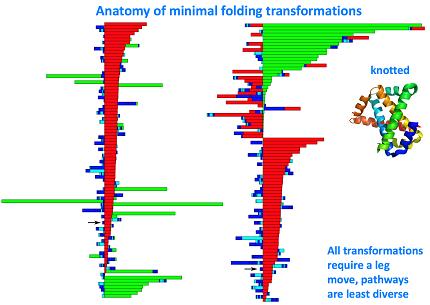
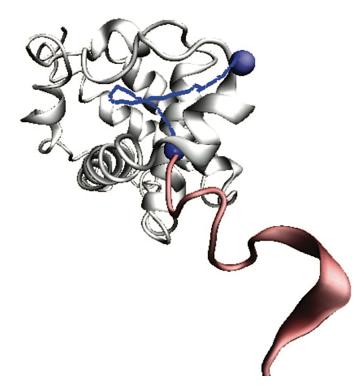
Two or more atoms cannot occupy the same space-- when such self-avoidance is accounted for, the trajectories that atoms take when a protein folds up can be highly non-trivial. Here is one such trajectory for a so-called C_alpha atom (blue bead) in a protein called apo-myoglobin, the minimal distance trajectory is curved and even doubles back on itself!

See Also:

Plotkin SS, "Generalization of Distance to Higher Dimensional Objects" Proc. Natl. Acad. Sci. 104, 14899 (2007)

Mohazab, AR, Plotkin, SS, “Minimal distance transformations between links and polymers: Principles and applications” J. Phys Condens Matter 20 244133 (2008)

Mohazab, AR, Plotkin, SS, "Minimal folding pathways for coarse-grained biopolymer fragments" Biophysical Journal 95 5496 (2008)

Mohazab AR, Plotkin SS, "Structural alignment using the generalized Euclidean distance between conformations" Int. J. Quant. Chem. 109, 3217–3228 (2009)

Das A, Sin BK, Mohazab AR, and Plotkin SS  "Unfolded protein ensembles, folding trajectories, and refolding rate prediction" J. Chem. Phys. 139, 121925 (2013)