

Next: Helmholtz free energy
Up: Boltzmann statistics
Previous: Boltzmann factor
The constant in (![[*]](cross_ref_motif.gif) ) can be determined by normalizing
the probability distribution i.e. requiring that
) can be determined by normalizing
the probability distribution i.e. requiring that
Let us define the canonical partition function
(
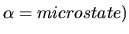
We find that the probability
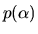 that a state is in a given
microstate
that a state is in a given
microstate
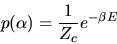 |
(17) |
Eq. (![[*]](cross_ref_motif.gif) ) is the canonical distribution. If
) is the canonical distribution. If
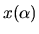 is the value of some physical property in microstate
is the value of some physical property in microstate 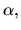 and
and
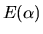 the energy of this state then the canonical
ensemble average is given by
the energy of this state then the canonical
ensemble average is given by
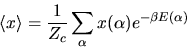 |
(18) |
Equation (![[*]](cross_ref_motif.gif) ) is a very useful formula, and we will give many
examples of its use.
) is a very useful formula, and we will give many
examples of its use.
Birger Bergersen
1998-09-14
![[*]](cross_ref_motif.gif) ) can be determined by normalizing
the probability distribution i.e. requiring that
) can be determined by normalizing
the probability distribution i.e. requiring that
![[*]](cross_ref_motif.gif) ) is the canonical distribution. If
) is the canonical distribution. If
![[*]](cross_ref_motif.gif) ) is a very useful formula, and we will give many
examples of its use.
) is a very useful formula, and we will give many
examples of its use.