

Next: The zeroth law of
Up: Boltzmann statistics
Previous: The historical origin of
Our starting point is the idea that one
can count the number of available states of a system. In principle, these are discrete quantum states. For a large system the states will
be very closely spaced.
The number of possible states with energy between
E and
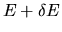 is
is
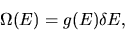 |
(1) |
where g(E) is the density of states.
Next, consider a closed system with fixed volume V, number of particles N, and energy E. In order to avoid problems associated
with the discreteness of the quantum states we take the energy to be
specified within a tolerance 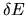 .
This tolerance should be
chosen so that for a large system the precise value of
.
This tolerance should be
chosen so that for a large system the precise value of 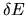 does not matter.
We do not know in which of the
does not matter.
We do not know in which of the 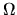 allowed states the system finds itself.
In fact, our fundamental assumption is that at equilibrium our ignorance
in this matter is complete, and that all the
allowed states the system finds itself.
In fact, our fundamental assumption is that at equilibrium our ignorance
in this matter is complete, and that all the
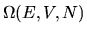 possible states are
equally likely, i.e. all memory of how the system was initially prepared
is lost, except for the values of the energy, volume, and number of particles.
We define the entropy as
possible states are
equally likely, i.e. all memory of how the system was initially prepared
is lost, except for the values of the energy, volume, and number of particles.
We define the entropy as
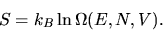 |
(2) |
Consider next an infinitesimally small change from an equilibrium state E,V,N to another,
slightly different, equilibrium state
E+dE,V+dV, N+dN.
The change in the entropy is then
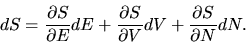 |
(3) |
The change in energy in this process is given by
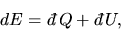 |
(4) |
We distinguish between two forms of energy heat and work.
Heat is a form of energy associated with random or
thermal motion of atoms and molecules. Consider a gas of
low density. The molecules will move in straight
trajectories until they collide with other molecules or the walls
of the gas container. After a few collisions it becomes
practically impossible to relate the velocity and position of the
molecules to the corresponding quantities at an earlier time. The
difficulty is not just the enormous amount of data required to
describe a large number of particles. A more fundamental problem
is the fact that after a few collisions the positions and the
velocities of the particles become extremely sensitive to the
initial conditions. A very similar situation occurs when throwing
an unbiased die or tossing a coin. In principle, it should be
possible to predict the outcome of the toss using Newton's laws
and the initial velocity and position. In practice, the
calculation will not be able to predict the behavior of
real coins, because initial conditions that give
rise to radically different outcomes are so close together that
the problem of specifying the intial conditions and parameters of
the problem with sufficient accuracy becomes severe. This type of
motion has been described as chaotic. Each particle is just
as likely to move in any direction as in any other, and the the
speed of the particles is frequently changing.
We also distinguish between the random
motion of a molecule and bulk (ordered) movement. An example of
the latter is the flight of a solid object such as a pebble
thrown in the air. We refer to changes in energy associated
with bulk motion or transport of matter as work. In (![[*]](cross_ref_motif.gif) )
)
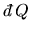 is the heat supplied to
the system and
is the heat supplied to
the system and
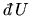 the work done on
the system. The internal energy E is a state variable and its differential
is exact, i.e. dE depends only on the initial and
final state and is independent of the process leading to the change.
On the other hand "heat" and "work" are not state variables
and the partition into heat and work depends on the process. Hence,
the difference in notation: dE, but
the work done on
the system. The internal energy E is a state variable and its differential
is exact, i.e. dE depends only on the initial and
final state and is independent of the process leading to the change.
On the other hand "heat" and "work" are not state variables
and the partition into heat and work depends on the process. Hence,
the difference in notation: dE, but
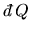 and
and
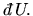 We have not yet defined the variables P, T and
We have not yet defined the variables P, T and 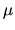 .
We want to do this
in such a way as to allow us to write
.
We want to do this
in such a way as to allow us to write
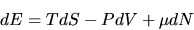 |
(5) |
or
We now define the temperature,
pressure, and chemical potential as
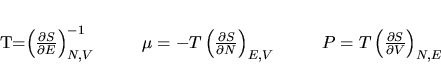 |
(6) |
It is important to note that our basic assumption is that all allowed states
are equally likely. The second law of thermodynamics now becomes the statement
that a closed system will tend to approach a macroscopic state which can be achieved
the most possible ways. The
conventional mathematical formulation of the second law (![[*]](cross_ref_motif.gif) ) on
the other hand only becomes an essentially trivial matter of definition.
We must next show that these definitions lead to familiar looking results-
otherwise they would not be useful.
) on
the other hand only becomes an essentially trivial matter of definition.
We must next show that these definitions lead to familiar looking results-
otherwise they would not be useful.


Next: The zeroth law of
Up: Boltzmann statistics
Previous: The historical origin of
Birger Bergersen
1998-09-14
![[*]](cross_ref_motif.gif) )
)
![[*]](cross_ref_motif.gif) ) on
the other hand only becomes an essentially trivial matter of definition.
We must next show that these definitions lead to familiar looking results-
otherwise they would not be useful.
) on
the other hand only becomes an essentially trivial matter of definition.
We must next show that these definitions lead to familiar looking results-
otherwise they would not be useful.